
Multiscale Modeling from the Electron to the Reactor
Matera group
Chemistry and material science are governed by physical phenomena on largely disparate time and length scales, each equipped with its own kind of modeling and corresponding simulation methods. On the smallest scales, the interaction of electrons and nuclei determine the properties of the system. Modern electronic structure theories allow to gain a deep insight into its functioning and to predict properties without employing material specific empirical parameters. On the other hand, most technical applications and experiments are influenced by macroscale phenomena like heat and and mass transport. Such aspects can not efficiently be simulated on the electronic structure level and must therefore be addressed by more coarse-grained models. The focus of the group is the development of multiscale modeling approaches and related numerical methods, which allow to bridge between electronic and atomic models and more coarse grained descriptions. The primary field of application is heterogeneous catalysis, but we have extended our research to different areas such as photo- and electrochemistry and charge and excitation transport.
First principles kinetic Monte Carlo
Many phenomena, like chemical reactions, are governed by the interplay of rare events, i.e. the duration of such events is much shorter than the time between two subsequent events. This separation of time scales can be addressed by modelling this interplay as Markov jump process and simulating sample trajectories using the kinetic Monte Carlo methodology. We are actively developing kinetic Monte Carlo methods and related software. We primary consider so-called first principles kinetic Monte Carlo models, in which the rate functions have been obtained from electronic structure calculations and reaction rate theories.
Atomistic-Continuum Coupling
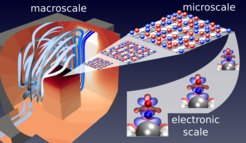
Albeit kinetic Monte Carlo substantially lifts the computational burden of fully atomistic simulations, it is still a molecular level method and the simulation of a whole reaction chamber or other kinds of devices is out of reach. During the last years, we have been working on coupling first-principles kinetic Monte Carlo models with continuum level solvers to describe macroscopic reactor response on a first principles basis. This kind of modeling allows to gain insights into the working principles of a material system, which are inaccessible by experimental data and phenomenological modeling alone. Originally, the approach was designed to address the interplay of macroscopic mass and heat transport with molecular scale effects in in situ characterization of single crystal heterogenous catalysts. Recently, we extended the approach to powder catalysts, but also to the coupling with nanoscale electromagnetic wave simulation to address the impact of inhomogeneous light absorption on heterogeneous photocatalysis.
Uncertainty quantification and sensitivity analysis
The input parameters of a computational model typically carry some kind of uncertainty. Either because they have been estimated from a necessarily approximate high-fidelity simulation, e.g. a quantum-chemical method, or because they inherit the uncertainty from the experimental data they have been derived from. Analyzing the impact of these uncertainties is the target of uncertainty quantification. Within this broad field, we particularly focus on developing methods for (global) sensitivity analysis, i.e. identifying those parameters which uncertainties have the largest impact on the model output. This information can then serve to more efficiently exploit resources. Only those parameters with large impact need to be determined with more accuracy, either by determining them with a more accurate comptational method or by running dedicated experiments. Besides this, sensitvity analysis can be used to gain a qualitative insight into the working principles of the model, for instance, rate-determining steps in a reaction mechanism. A special focus of our method developments here are approaches which are suited for Monte Carlo simulation models and to apply them to investigate the error propagation in multiscale models, particularly first principles based kinetic models.
High-dimensional discretization

The need for high-dimensional discretization is a recurrent problem in our research. Such problems appear, for instance, in uncertainty quantification, atomistic-continuum coupling using surrogate models or the solution of dynamical laws for stochastic or quantum many-particle systems. The challenge is here, that most numerical methods are affected by the so-called curse of dimensionality. That is the computational effort to achieve a certain target accuracy increases exponentially with the dimensionality. Monte Carlo methods are well-known to overcome the curse with the kinetic Monte Carlo method as a special case, which avoids the need to solve Markovian master equations. In uncertainty quantification, we typically employ Quasi Monte Carlo sampling, which more efficiently explores parameter spaces than plain Monte Carlo in many cases. However, both kind of approaches target at some kind of integration and not all problems can efficiently be mapped onto an integration problem. Besides testing the usual suspects from machine learning, we therefore also employ and actively develop approaches which can be used for function approximation such as adaptive sparse grids or tensor network approaches. These are used to to create surrogate models, where we focus on extensions which efficiently cope with stochastic base models, or with the solution of particular classes of master and Schrödiger equations.

